MUSIQUE CONTEMPORAINE - La musique sérielle et le dodécaphonisme

MUSIQUE CONTEMPORAINE - La musique sérielle et le dodécaphonisme

Le besoin d’établir l’existence d’une « démocratie » sonore, c’est-à-dire de définir les bases d’un langage où la « tyrannie de la dominante » ne s’exercerait plus, se fit sentir très tôt. Sans remonter jusqu’au chromatisme de Cypriano de Rore (1516-1565) ou de Gesualdo da Venosa (1560 env.-1614), des faits comme l’apparition de l’accord de septième diminuée ou de quinte augmentée répondaient obscurément à ce besoin. De même, la prolifération des « notes à côté », qu’elles fussent résolues ou non, montrait une volonté d’émancipation qui s’affirmait avec chaque génération.

En harmonie classique, chaque accord peut être identifié grâce à un chiffrage conventionnel (basse chiffrée). À la fin du XIX^e siècle, notamment avec le chromatisme wagnérien et sa « mélodie infinie », les règles de l’analyse harmonique ne suffisent plus pour rendre compte, de manière satisfaisante, de l’émiettement que subit la tonalité, voire pour chiffrer avec certitude certains agrégats sonores, tel l’accord fameux du prélude de Tristan . Mais l’ensemble du problème n’est posé clairement que dans les premières années du XX^e siècle. La plupart des musiciens acceptent alors la « mort du principe tonal » et écrivent une musique atonale (ainsi les accords fréquents de neuvième et de onzième, le modalisme de Claude Debussy, la polytonalité d’Igor Stravinski ou de Darius Milhaud, jusqu’aux modes à transpositions limitées d’Olivier Messiaen, etc.). Néanmoins, aucun système d’écriture ne prétend remplacer la vieille organisation tonale avec à la fois autant de précision et de généralité que le dodécaphonisme, surtout dans ses développements sériels.

Le dodécaphonisme est la doctrine qui correspond aux différents systèmes d’écriture utilisant les douze sons de la gamme chromatique tempérée sans référence à la tonalité. Josef Matthias Hauer et Arnold Schönberg ont attaché leur nom à cette période de rénovation de l’écriture musicale.

1. Gamme tempérée et structures élémentaires de l’harmonie classique

Pour bien comprendre ce que fut l’apport de la musique « à douze sons », il convient de faire auparavant une rapide étude du langage tonal, fondement de la musique occidentale traditionnelle. Ce langage utilise douze sons qui se renouvellent sur environ huit douzaines, nommées octaves. La théorie et la pratique de l’écriture musicale sont conçues pour que les éléments de l’ensemble ainsi défini soient traités comme des sons tempérés. Dès l’instant, en effet, où la musique devint polyphonique, il fallut bien établir une approximation dans le phénomène de la résonance. Aux sons harmoniques naturels qui prolifèrent avec chaque fondamentale, de telle sorte, par exemple, que la quinte d’un fa diffère sensiblement de la tierce d’un la bémol, on fut obligé de substituer des sons tempérés, c’est-à-dire, pour reprendre cet exemple, de définir un son unique nommé do , valable comme quinte de fa et comme tierce de la bémol. On en vint ainsi à définir la gamme chromatique tempérée comme un ensemble de sons tel que, étant donné F la fréquence du plus grave d’entre eux, on obtienne la fréquence des suivants en multipliant F par une puissance de 2 fractionnaire, de dénominateur 12.

Le catalogue des fréquences fondamentales utilisées en musique s’échelonne grosso modo entre 32 et 2 048 Hz, ce qui correspond à peu près au clavier d’un piano. À ces fréquences correspondent des hauteurs , qui en sont le logarithme de base 2.

On peut sans inconvénient, en employant douze chiffres, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, X, Z, noter les douze hauteurs repérables dans une octave et écrire, en unités de premier ordre pour la note, de second ordre pour l’octave:

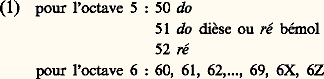etc.

Une hauteur ainsi notée est immédiatement convertible en la fréquence correspondante par la formule f (xy ) = 2^{(x +y /12)}

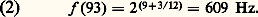La musique classique se conformait à un modèle mélodique, la gamme, sélection opérée dans l’ensemble des hauteurs, telle que, x étant un élément quelconque de cet ensemble, on ait:

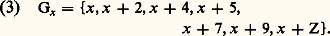Elle se conformait d’autre part à un modèle harmonique tel que, pour un son quelconque x , en se bornant aux trois premières résonances différentes de l’octave, on entendît toujours, dans un ordre indéterminé, en même temps que ce son, les sons x +4 et x + 7; on peut donc écrire en nommant Hx ce modèle:

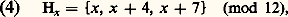ce qui pour x = 0, par exemple, donne:

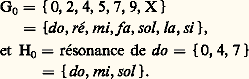Cette organisation favorise l’émergence de trois accords, celui de tonique , celui de sous -dominante et celui de dominante , c’est-à-dire respectivement Hx =x , x + 4, x + 7, H^x +5 =x , x + 5, x + 9, Hx +7 =x + 2, x + 7, x + Z qui sous-tendent le discours musical en établissant une hiérarchie parmi les douze notes de la gamme chromatique.

C’est cette hiérarchie que la musique « à douze sons » se propose d’abolir en édictant des règles propres à établir un discours où la prédominance de ces accords ne se fasse plus sentir. Josef Matthias Hauer, puis Arnold Schönberg furent les théoriciens de ce mouvement, né à Vienne dans les années 1920.

2. Le dodécaphonisme de J. M. Hauer

Josef Matthias Hauer, né en 1883 à Wiener-Neustadt, en Autriche, était instituteur. Autodidacte dans le domaine musical, il écrit dès 1911 dans un système à douze sons parfaitement cohérent, qu’il précise en 1918 sous le nom de Zwölftongesetz . Il en expose les principes dès 1920 dans une brochure intitulée Vom Wesen des Musikalischen (De l’essence du fait musical ), qu’il continue à mettre en pratique jusqu’à sa mort en 1959. « Il n’y aura plus, en « musique atonale », écrit-il dans cet ouvrage, de tonique, de dominante, de sous-dominante, de degrés, de résolution, de consonances, de dissonances, mais seulement les douze intervalles égaux d’un espace musical homogène. » Sa « gamme », car on ne peut plus placer ce mot qu’entre guillemets, ne se compose donc que de douze demi-tons tempérés. La mélodie atonale nouvelle éliminera donc avec une intransigeance égale l’émotion physique ou sensuelle au même titre que la vulgarité ou la sentimentalité. La loi immuable de la musique atonale, sa règle d’or, consiste en ce que les douze sons de la gamme tempérée doivent tous être joués et sans cesse repris. Ainsi, le désir manifesté par Hauer de soustraire le discours musical aux lois de la résonance débouche, tout naturellement, sur une ascèse sonore ignorée jusqu’à lui, une ascèse qu’ignorera d’ailleurs Schönberg. Selon les grands principes de la polyphonie hauérienne, un son nouveau ne peut apparaître dans le discours que si celui qui le précède dans la même voix est à distance d’un ton ou d’un demi-ton, supérieur ou inférieur. Ainsi, le son sol , par exemple, doit être précédé, soit d’un fa dièse, soit d’un la , soit d’un sol dièse.

Quatre sons initiaux sont présentés simultanément, formant généralement un accord de septième majeure ou mineure. On a par exemple: do - mi - sol - si . À ce premier complexe en succède un deuxième (tabl. 1) ne différant du premier que par un son introduit comme il a été dit. Suit un troisième complexe ne différant du deuxième que par un son et ainsi de suite jusqu’à ce qu’on retrouve le premier complexe, comme dans l’exemple donné par le tableau 2.

On a ainsi la « série » do , do dièse, ré , la dièse, sol dièse, fa , ré dièse, fa dièse, la , mi , do , sol , si , qui sera à la base de toute l’œuvre.

Les quatre sons de chaque complexe permutent entre eux deux à deux, la ligne mélodique résultant, dans chaque voix, de cette opération devant se lire en suivant les traits qui matérialisent ici cette permutation (do , mi , mi , si pour la voix qui débute par do ); le tableau 3 représente un des premiers complexes possibles. Pendant l’introduction du son nouveau, deux autres sons permutent de la même façon, mais cette permutation ne doit pas affecter la ligne où se trouve le nouveau son (tabl. 4).

Le tableau 5 représente la polyphonie à quatre voix qui résulte de ces différentes opérations si l’on suit les lignes qui indiquent les permutations des sons. À partir de ce schéma de permutations, il suffit d’affecter à chacune des colonnes de sons une même durée, choisie arbitrairement, pour se trouver en présence d’une partition où sont définis sans ambiguïté des fréquences (à l’octave près) et des rythmes. Pour chaque colonne valant une double croche, par exemple, on a successivement dans la première ligne deux croches (si et sol ), une croche pointée et une double croche (mi et sol ), dans la deuxième ligne successivement une croche et deux doubles croches (sol , si et mi ), puis deux croches (sol et si ) de sorte que l’exemple ci-dessus peut être réalisé de la façon suivante:

L’œuvre consiste en un nombre fixe d’expositions des douze complexes dont la construction a été précisée ci-dessus, donnant lieu à des permutations différentes. Certains dessins mélodiques sont soulignés par leur doublure à l’octave supérieure ou inférieure.

Le système dodécaphonique de Josef Matthias Hauer suscita peu de curiosité à l’époque où il fut conçu, et la vie de son inventeur fut toujours marquée par une grande détresse matérielle. Cependant, par la rigueur de sa pensée, par les possibilités qu’ouvre son système d’écriture à une mécanisation de la composition musicale, il annonce les recherches les plus récentes. « Son idée dominante, dit le musicologue H. H. Stuckenschmidt, qui était de composer une musique désincarnée, à la fois spirituelle et abstraite, et purement atonale, n’a jamais franchi un cercle étroit. Mais sa personnalité comme son art étaient d’un authentique prophète et possédaient une vraie grandeur. »

Parmi ses successeurs, on peut citer Herman Heiss et Jef Golyscheff, auteur de la Zwölftondauermusik (musique dodécaphonique continue).

3. Arnold Schönberg et la musique sérielle

La musique sérielle, ou plutôt le principe sériel, est une extension et une généralisation de la méthode d’écriture dite dodécaphonique. Le système tonal établissait une dualité dans le discours sonore en se conformant en même temps à deux modèles: l’un, la gamme, contrôlait l’horizontalité; l’autre, la résonance des fondamentales successives, contrôlait la verticalité. Arnold Schönberg s’est efforcé de définir une structure unificatrice qui fût à même de contrôler l’une et l’autre à la fois. Il en a trouvé le principe dans la série (Reihe ). Il n’y a plus désormais de mélodie et d’harmonie, mais un concept global qui les réunit en une seule entité. « Les éléments d’une pensée musicale – mélodie, rythme et harmonie – sont reliés entre eux d’une part au moyen de sons qui se succèdent l’un à l’autre horizontalement, d’autre part au moyen de sons synchrones verticalement » (Theory of Harmony ).

Si l’on contraint les douze éléments de la gamme tempérée à apparaître au sein de la polyphonie dans un ordre donné, on obtient une série: une série est donc définie à l’octave près. Théoriquement, elle peut être choisie parmi les 12! = 479 001 600 permutations de douze sons (12! s’énonce « factorielle 12 » et vaut 1 憐 2 憐 3 憐 4 憐 5 憐 ... 憐 12). Pratiquement, cependant, Schönberg et les autres théoriciens préconisent un choix parmi celles qui peuvent offrir des possibilités architectoniques (symétries des intervalles, caractères « thématiques », possibilités de développement, etc.). Cet ordre imposé confère à la série un pouvoir organisateur qui est utilisé pour donner une cohérence au discours musical.

Lorsqu’on énonce les éléments d’une série en les lisant de gauche à droite, on définit sa forme dite fondamentale (F). Voici celle qu’utilise Schönberg dans ses Variations pour orchestre :

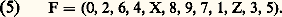Les éléments de F lus de droite à gauche constituent la forme récurrente (R):

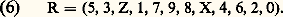Les symétriques des éléments de F, lus de gauche à droite, constituent la forme renversée (V) de la série:

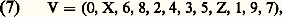qui, lue de droite à gauche, donne la forme récurrente -renversée (RV):

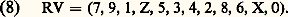Chacune de ces quatre formes peut être transposée douze fois par l’addition d’une constante, et l’on a par exemple:

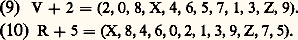« Exposer » une des quarante-huit formes d’une série donnée, c’est disposer la polyphonie de telle façon que les douze notes y apparaissent dans l’ordre défini par cette forme, étant entendu que l’apparition simultanée de deux ou davantage d’éléments consécutifs est licite. Si donc nous considérons un tableau rectangulaire, dont les lignes correspondent aux voix de la polyphonie ou à des instruments, les colonnes à des dates rangées par ordre croissant, l’exposition d’une des quarante-huit formes de la série peut être représentée schématiquement par l’énumération des douze éléments de cette forme, en suivant un itinéraire passant par douze cases et tel qu’il ne tourne jamais vers la gauche. Voici un exemple d’itinéraire conforme à cette définition dans un tableau comportant cinq voix et seize dates (soit cinq lignes et seize colonnes).

Énumérant dans les douze cases parcourues par cet itinéraire, les douze notes de R + 5 par exemple, on obtient:

Les opérations décrites ci-dessus définissent douze attaques de douze sons dont la prolongation n’obéit à aucune loi écrite. Quant à la localisation de ces douze sons dans des octaves, elle doit, bien entendu, tenir compte de la tessiture des instruments employés. L’observation des textes montre que les intervalles très disjoints y sont généralement préférés aux intervalles courts. Compte tenu de ces remarques, le tableau précédent peut donner lieu, en considérant par exemple que les seize dates correspondent à celles qui seraient définies par seize doubles croches successives, à la réalisation suivante:

Plusieurs formes de la série peuvent être exposées en même temps. On doit alors éviter la faute nommée « fausse relation d’octaves », qui consiste à faire entendre une même note dans des octaves différentes, soit à la même date, soit à des dates suffisamment rapprochées pour que l’oreille le décèle. Le compositeur choisit généralement une série dont les caractères lui offrent des possibilités de développement remarquables. Ainsi les six premiers sons de l’exemple (5), soit 0, 2, 6, 4, X, 8, génèrent par renversement, récurrence et transposition à la quarte, les six derniers, soit 9, 7, 1, Z, 3, 5, de sorte qu’on a:

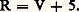Si, au lieu de considérer les sons, on considère leurs rapports réciproques, c’est-à-dire les intervalles qui les séparent, la technique sérielle se trouve encore élargie.

Les lois définissant l’apparition des sons sont les seules qui aient jamais été formulées. Si elles sont nécessaires à l’élaboration d’un discours musical qui ne soit pas entaché de réminiscences tonales, elles ne sont pas suffisantes pour lui donner la physionomie particulière à laquelle nous ont habitués Schönberg et ses disciples. On décèle dans leurs œuvres des habitudes comme la préférence donnée presque systématiquement aux grands intervalles mélodiques, répondant à un souci de dispersion de la matière sonore pour accentuer l’impression de dépaysement hors de l’univers tonal.

Les deux autres grands noms de ce qu’on a appelé la « nouvelle école de Vienne » sont les disciples les plus importants de Schönberg, Alban Berg (1885-1935) et Anton von Webern (1883-1945). Ils appliquèrent, chacun avec son tempérament propre, la technique sérielle, sans y apporter d’extension qui mérite d’être ici exposée en détail. Il faut cependant noter l’attirance de Webern pour les séries tronçonnées, dont les intervalles sont choisis de façon qu’un tronçon soit le symétrique d’un autre: la série arrive ainsi parfois à se confondre avec son renversement. Tiré du Quatuor opus 28, en voici un exemple:

récurrence de la forme fondamentale ou renversement et transposition au cinquième demi-ton supérieur: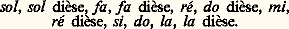

Hormis les aspects techniques de cet ordre, l’originalité propre des œuvres de Berg ou Webern peut être une preuve de la souplesse et de la richesse de la musique à douze sons. On peut citer également, dans le prolongement de l’école de Vienne, les noms de Hanns Eisler, Hermann Zenk, Leopold Spinner, Paul Dessau, Martin Vogel.

4. Extension de la notion de série

Dans les premiers temps, le sérialisme n’eut pas de large audience en dehors de l’école de Vienne, sauf exceptions importantes comme Luigi Dallapiccola et Ernst Krenek. Dans le courant des années cinquante, la notion de série fut étendue aux autres composantes du son, la méthode se généralisant avec des compositeurs comme Wilton Babbit, Pierre Boulez, Luigi Nono ou Karlheinz Stockhausen. La technique sérielle fut aussi utilisée par des compositeurs « établis » tel que Igor Stravinski (In memoriam Dylan Thomas ).

Le premier compositeur à appliquer rigoureusement la méthode sérielle aux hauteurs, aux durées et aux intensités est Olivier Messiaen, dans une œuvre pour piano intitulée Modes de valeurs et d’intensités . D’une façon générale, on vit apparaître des séries de durées, de timbres et d’intensités, entre lesquelles s’établirent des « interactions ». Ainsi, les représentants de ce que l’on a appelé l’école post-sérielle instaurèrent une interdépendance des quatre composantes du son, et la série devint « le germe d’une hiérarchisation fondée sur certaines propriétés psychophysiologiques acoustiques, douées d’une plus ou moins grande sélectivité, en vue d’organiser un ensemble fini de possibilités créatrices liées entre elles par des affinités prédominantes par rapport à un caractère donné » (Pierre Boulez).

On peut citer ici les noms de Luciano Berio (Nones pour orchestre, 1954), Pierre Boulez (Structures I pour 2 pianos, 1952), Karlheinz Stockhausen (Kontra-Punkte , 1952), ainsi que ceux de Luigi Nono, d’Henri Pousseur et de Jean Barraqué.

Bien que la technique sérielle ait pratiquement été abandonnée par la génération des musiciens qui se manifestèrent à partir des années soixante, la tradition a été maintenue dans son intégrité par des pédagogues de grande valeur comme Max Deutsch ou Josef Rufer. D’ailleurs, quel que soit le jugement que l’on porte aujourd’hui sur l’intérêt de la technique sérielle, il faut avouer qu’une voie nouvelle a été ouverte et que de nombreux aspects de la musique contemporaine, telle la composition musicale par ordinateur, n’auraient pu être envisagés si de nécessaires habitudes d’écriture rigoureuse n’avaient été introduites en musique dès l’apparition de la technique dodécaphonique.

Encyclopédie Universelle. 2012.